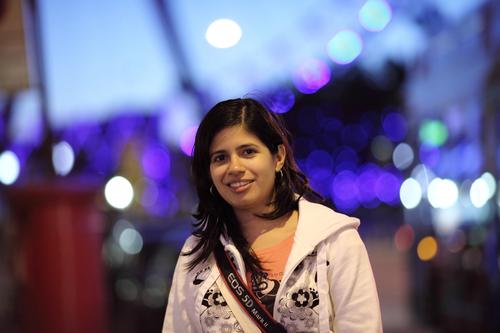Here is a portrait with large bokeh balls in the background (from Wikimedia):
The size of the bokeh balls in the background of a shot like this is determined primarily by the size of the lens aperture, technically known as the entrance pupil. The diameter of the entrance pupil is the focal length divided by the F-number. The photograph above was taken with a 135mm lens at f/2. The F-number is 2 and the entrance pupil is 135/2 = 67.5mm.
If the background is distant (say, at least ten times as far away as the subject), then the bokeh balls from bright points of light in the background will be approximately the same size as the entrance pupil, i.e. 67.5mm for this example. The size is measured on the same scale as the subject (on which the camera is focussed). With human faces, the inter pupillary distance (from the centre of one eye to the centre of the other) averages around 62mm for women and 64mm for men. This gives a very approximate idea of the scale on which to measure the blur size.
For any camera lens on any camera, the maximum size of the bokeh balls produced by points of light in the background is always equal to the diameter of the entrance pupil, which is the focal length divided by the F-number (also called the F-stop or simply the aperture). The maximum size bokeh balls will occur If the background is at infinity. In practice, this means more than about ten times as far away as the subject. The closer the background is to the subject the smaller will be the bokeh balls and, in general, the less blurred will be the background.
I haven't mentioned subject distance because it is not relevant to the maximum size of the blur. For a background at infinity, the size of the blur remains the same relative to the subject whatever the distance from subject to camera. As the subject moves further away from the camera, the size of the subject in the frame reduces and the size of the blur reduces in proportion.
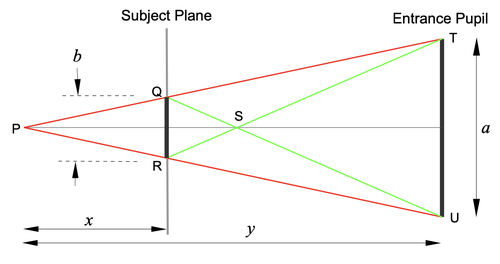
Entrance Pupil
The entrance pupil is the hole that you see when you look into the front of the lens. The light entering that hole is used to form the image on the sensor. Light rays that do not enter the entrance pupil hit the edges of the internal elements of the lens and do not play any part in forming the image.
From left to right: 12mm f/2.8 EP=4.3mm; 45mm f/1.8 EP=25mm; 75mm f/1.8 EP=42mm; 25mm f/1.4 EP=18mm; 9mm f/4 EP=2.2mm (the zoom lenses are at the short end of the zoom).
For wide-angle lenses in particular the front element of the lens is often much larger than the entrance pupil.
See the next post for details of how to calculate the size of the blur for any background distance and any subject distance.