Your formula for the disc of confusion is not quite correct. For it to work correctly, D must be the distance from the OOF object to the aperture. Here is a diagram that (hopefully) will make things clearer:
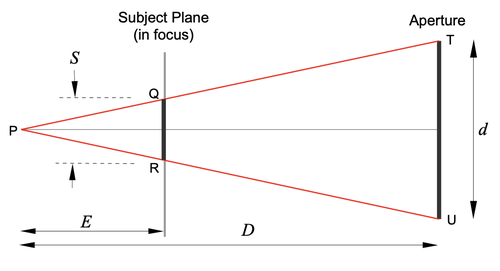
P is a point on the surface of the moon. The point P appears as a blur that extends from Q to R in the plane of focus (the mountain range 4km away).
E is the distance from the OOF point P to the plane of focus, while D is the distance from the OOF point P to the aperture (indicated by the line from T to U).
S is the distance from Q to R, which is the size of the blur produced by the OOF point P in the plane of focus, i.e. the disc of confusion.
The plane of focus (subject plane) is parallel to the plane of the aperture, hence the triangles PQR and PTU are similar.
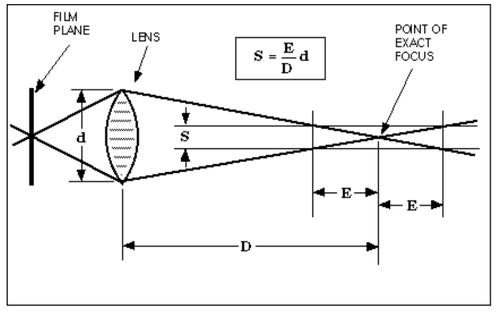
Hence S = E/D*d.
For your example, d = 45mm, D = 400,000km and E = 399,996km, so S = 45mm. This is the disc of confusion produced in the plane of focus (4km away from the camera). 45mm will not be a visible blur at 4km distance, so the moon will look sharp if the camera is focused on mountains 4km away.
If the plane of focus is at the surface of the moon and the mountains 4km away are now OOF, then D (the distance from the OOF point to the aperture) is now 4km.
E is the distance from the OOF point to the plane of focus, so E is now 399,996km. Hence the disk of confusion is now 399,996/4*45mm, which is 4.5km (near enough). Now 4.5km is too small a distance to be distinguished on the surface of the moon (with an ordinary camera and 1000mm f/22 lens), so the mountains at 4km distance will also appear sharp.