The results depend not only on the ratio of exposure and cycle periods, but the depth of the cycle. When lights cut off and on quickly during a cycle, the mismatches with exposure time are the boldest. When the cycle is shallow due to phosphors or circuitry, then small mismatches may be more tolerable, except that with video, a luminance band that is shallow enough to be ignored by the brain in a still may be more visible when it is rolling through the frame.
-
-
Here's an example that shows the acceleration:
blog.kasson.com/d850/how-fast-is-the-nikon-850-electronic-shutter/
-
Yes, that appears to be normal. See e.g.: dprevived.com/t/new-ways-with-shutter-travel-time-measurement/3402/
There the shutter accelerates from about 5m/s at the start of exposure to about 10m/s in the centre of the frame, and remains at about 10m/s until the end of the frame.
I have similar examples from other cameras.
If the acceleration profiles of the first and second curtains can be sufficiently accurately matched, the exposure time is basically the delay between triggering the first curtain, and triggering the second curtain.
At 1/8000.0 s, and 10m/s shutter, the gap between the first and second curtains is 1.25mm.
At 5m/s, the gap between the first and second curtains is 0.625mm.That's with a premium, fast-moving FF shutter that allows 1/320 X-Sync. (Similar performance to D850 shutter).
I haven't tried precise modelling, but I don't think EFCS-style bokeh truncation problems are possible at realistic f/numbers. Exposure uniformity is an issue, though - the exposure time varies across the frame at high shutter speeds.
-
Yes - the worst lighting for flicker is low-duty-cycle Pulse-Width-Modulation - strobe-like lighting. That can happen with domestic dimmable LEDs in some cases, but unfortunately also with professional (e.g. theatre) dimmable LED lighting where PWM is used to extend the dimming range below the range available from analogue regulation of the switching power supply that drives the LEDs.
-
@JohnVickers has written:@JohnSheehyRev has written:@PHz has written:
the main worry seems to be the clash between mains frequency and pictorial outcome, If not near 1/60 or 1/50 will a small deviation really matter?
The results depend not only on the ratio of exposure and cycle periods, but the depth of the cycle. When lights cut off and on quickly during a cycle, the mismatches with exposure time are the boldest. When the cycle is shallow due to phosphors or circuitry, then small mismatches may be more tolerable, except that with video, a luminance band that is shallow enough to be ignored by the brain in a still may be more visible when it is rolling through the frame.
Yes - the worst lighting for flicker is low-duty-cycle Pulse-Width-Modulation - strobe-like lighting. That can happen with domestic dimmable LEDs in some cases, but unfortunately also with professional (e.g. theatre) dimmable LED lighting where PWM is used to extend the dimming range below the range available from analogue regulation of the switching power supply that drives the LEDs.
I'm glad I'm a hobbyist, and not a person who is paid to take quality photos in venues with crap lighting systems.
I have a hatred of mains-frequency deep cycling that predates experience with slow-rolling shutters. I discovered back in the '70s that automobile AM radios often had amazing sensitivity and tuning selectivity and I used to listen to stations 200-300 hundred miles away during the daytime and about 1500 miles at night, in my college dormitory with a car radio powered by a 12V filtered power supply. Then, they updated the lighting in my dorm with dimmers, and I could only hear local stations when my roomates wanted dimmed light.
-
@BernardDelley has written:@BernardDelley has written:@JohnVickers has written:
If you set "1/60" shutter speed, what exposure time do you expect?
I doing consistency checks on shutter times, I came to the conclusion that Nikon DSLR had 1s to quartz precision and the other times in precise
powers of two, respectively 2^1/3, steps of actual time values. So 1/60s nominally is actually 1/64s etc. I assume other cameras do the same. (nominal 30s was 32s -0+0.3 hand stopped on shutter sounds)I could not resist checking again on my earlier tests about exposure precision mentioned in my previous post here. While it may barely matter for much of normal photography, it does for scientific purposes like measuring external quantum efficiency of a sensor. There you like to have things accurate, if you can.
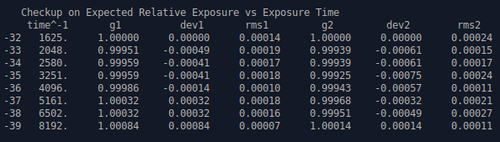
In today's test with result reported below, I used two LED panels illuminating white paper with 'continuous light' and took images with a D850 and a 105mm lens fully open at f/1.4 using electronic shutter 'silent lifeview SL1 mode'. Exposure at 1/1600 s nominal resulted in about 22'000 electrons per pixel and correspondingly less for shorter exposure times. My reported averages for Bayer green 1 and for green 2 are the average coming from 4 takes where the pixel values of the 10000 central pixels of the Bayer subset were averaged. From the 4 takes I can know how precise these average readings are, this is reported as rms1 resp rms2.
The table shows these 4take averages normalized to the shown assumed exact exposure time and the average count one from the first take. This allows to see the deviation from expected exposure easily.
The greatest seen rms deviation was at 0.03%, which is close to expectations from Poisson statistics.
If you have 22000 e- per green pixel, the pixel standard deviation is about sqrt(22000) ~= 148 e-
If we then average these 10000 green pixels, the standard deviation of the average (attributable to shot noise) will be about 148/sqrt(10000) ~= 1.48 e-
The ratio of the standard deviation (attributable to shot noise) to the mean is about 1.48 / 22000 = 0.000067 (about 0.0001 EV).
Which is somewhat below the "rms" shot-to-shot noise that you are seeing (except maybe at high shutter speeds).
Getting the variation in the standard deviation of the replicates down to a level where we can reason about the standard deviations of different treatments needs quite a few replicates: The 𝜒2 confidence intervals for the population standard deviation start out very wide.
Try: www.statskingdom.com/confidence-interval-calculator.html with 'type:' "Standard deviation confidence interval" and 'Data is:' "SD, n".
This is why I usually end up doing 8 or 16 replicates of each test condition. (And why I use an intervalometer a lot in these tests).
With 4 replicates, a 90% confidence interval for the population standard deviation is [0.62s, 2.92s].
With 8 replicates, a 90% confidence interval for the population standard deviation is [0.71s, 1.80s].
With 16 replicates, a 90% confidence interval for the population standard deviation is [0.77s, 1.44s].- Where s is the sample estimate of the population standard deviation.
(This being the internet, for all I know, you could be a professor of statistics. If I'm teaching you to suck eggs, I apologise.)
@BernardDelley has written:A part of it may be due to residual time dependence of the light sources and residual jitter of the electronic shutter.
Yeah.
@BernardDelley has written:The hypothesis that a common "32kHz" quartz clock may be used, uttered in my previous post is clearly dismissed, as this would result in a~6% deviation for the 1/5000s exposure.
Edited: I misunderstood the number of pixels in the patches Bernard is using - I thought they were 25000 pixels, but it seems they are 10000 pixels.
Edited: Hurried to fix the above, and made another silly error. -
@BernardDelley has written:@JohnVickers has written:@BernardDelley has written:@JohnVickers has written:
You were using an f/1.4 lens at f/1.4. I was using an f/2 lens at f/2. The difference in Numerical Apertures might go some way towards explaining the differences in our results.
It is a shutter specimen individual thing. All my cameras have different exposure stretch at 1/8192s with mechanical shutter:
my D7200 29% yours 15% , my D500 11% , D800 13% , D850 10%, Z7II 19% (f/1.4 and f/4).
My reply to Jim showed that there is no f ratio dependence for this exposure stretch of significance.This is what I got on D7200 with a 150mm lens at f/5.6:
The lens is Sigma 50-150 f/2.8 DC OS. At 150mm it's truly telephoto. Bill Claff doesn't have a model for it, but I'm guessing that the exit pupil is 10cm+ from the focal plane.
I halved the height (but not width) of my patch size to give 512x256, as well as using a larger f/ number.
That reduced the "exposure stretch" on my D7200 to 11%.
This makes me more confident about some surprising electronic shutter speed measurements I made on Panasonic S5 (more later) - in these measurements, the electronic shutter speeds have this kind of "exposure stretch". Perhaps to match the mechanical shutter?
In any case, if we're not seeing anything close to 1/8192 over a tiny patch at the centre of the frame, when are we supposed to see it ?
You would have to look into the statistics of your averaged 16 measurements to know about the significance.
Can you be more explicit? Do you mean statistical significance?
The differences I get are quite large compared to the standard deviation of the replicates. The replicate standard deviation estimate is the "G sd EV" column. We can expect the mean EVs for each case to be distributed with sd roughly a quarter of the corresponding "G sd EV" value.
With 16 replicates per treatment, a 90% confidence interval for the treatment mean is: (sample mean) +/- 0.44*(replicate standard deviation).
Stopping down the 15-150 to f/5.6, compared to using the 60mm f/2 wide open adds about 0.01EV noise. (I don't have a manual-only lens that I can use on F-mount).
The D7200 tests I did went down to 11EV (above 1DN). At 11EV, the variation in the replicate means attributable to Poisson noise is in the 8E-5 EV ballpark. So negligible. I could/should use more of the available dynamic range.
I mentioned black level errors before. If I have a 0.5DN black level error at 11EV, that's a 0.00035EV error; if I have a 0.5DN black level error at 6EV, that's a 0.01EV error in a measurement near 6EV. That's at the level of effects I'm trying to detect. I could try gettting more fancy with the statistics, but they would be less robust.
@BernardDelley has written:At least the stretch is "monotonic" roughly doubling when halving the shutter speed. This is consistent with a systematic, constant, lateness of the second curtain. It may be telling that all our cases see lateness. Maybe that is intentional: 50% early would be a full stop underexposed: about 1/16000s, 50% late is roughly half a stop overexposed: the tolerance is more favorable to the late side.
After our results, I do not expect seeing 1/8192s with a mechanical shutter.
Me neither.
@BernardDelley has written:What we see is less than a third stop off the mark, which is perfectly acceptable for a maximum speed in practical action photography. We can see more accurate shutter speeds with the electronic shutter, where I confirmed it for the D850 and Z7II. One can understand that Nikon only provides an electronic shutter with top models Z9 and Z8, now that they can make a reasonable flash sync speed of 1/200s with electronic shutter.
BTW, I use a 200x200 patch which gives 10'000 pixels in each of the four Bayer subsets. And the 10'000 pixels of the set let expect a 100 fold improved SNR for the DN average as compared to the single pixel DN.
My argument for independence of exposure stretch against aperture, may imply a stretch dependence along the shutter movement direction. One would have to recheck this and perhaps set up a measurement with small patches along the way.
- Which is exactly what I was trying to do when I fell down this rabbit hole. I was particularly looking for EFCS problems.
@BernardDelley has written:By lack of time, I loose interest for more detail on exposure stretch with mechanical shutters. Surely there are further subtleties and catches with electronic first shutter curtain. Exposure stretch is not a practical problem, even for for my repaired D7200. I learnt, that I can get precise exposures with electronic shutter up to the highest speeds. One might use this to see how consistent stopping down can be with specific lenses: preliminary results taken along with my MTF measurements suggest fairly accurate for electronically controlled apertures.
-
A related question:
I was testing a lens in bright sunlight the other day.
i had set the shutter time to 1/6000sec - Manual mode.
When converting RGB and displaying the EXIF in an app or two, I saw two shutter-related values: 1/6000sec and 1/66sec.
The 1/66sec value was called "Integration Time".
Anybody know what that is exactly? Any references?
The camera is a Sigma SD9 but I've seen the matter mentioned on other cameras while I was briefly searching for info ...
-
@xpatUSA has written:
A related question:
I was testing a lens in bright sunlight the other day.
i had set the shutter time to 1/6000sec - Manual mode.
When converting RGB and displaying the EXIF in an app or two, I saw two shutter-related values: 1/6000sec and 1/66sec.
The 1/66sec value was called "Integration Time".
Anybody know what that is exactly? Any references?
The camera is a Sigma SD9 but I've seen the matter mentioned on other cameras while I was briefly searching for info ...
My first guess is that this is how long each photosite was actively "on", taking charge; IOW, the underlying e-shutter "exposure" time which is partially (mostly, in this case) masked by the mechanical curtains. That number is what you might use to predict dark current noise. Remember, in any digital camera with mechanical shutter curtains, there photosites are active for far longer than they are exposed to light, with fast shutter speeds.
-
Thanks John.
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
-
@xpatUSA has written:
Thanks John.
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
John Sheehy's idea makes more sense.
The time between the earliest exposure of any part of the sensor to the latest exposure of any part of the sensor =
(Shutter travel time AKA rolling shutter) + (exposure time).Your SD9 has an X-sync limit of 1/180. So the Shutter travel time is less than 5.5ms. Probably about 4.8ms.
Your exposure time is "1/6000", or something near 0.2ms.
So the time between the earliest exposure of any part of the sensor to the latest exposure of any part of the sensor =
something less than 6ms, probably a bit less than 5ms.Definitely nowhere near the 15ms implied by "1/66" s.
-
@JohnVickers has written:@xpatUSA has written:
Thanks John.
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
John Sheehy's idea makes more sense.
The time between the earliest exposure of any part of the sensor to the latest exposure of any part of the sensor =
(Shutter travel time AKA rolling shutter) + (exposure time).Your SD9 has an X-sync limit of 1/180. So the Shutter travel time is less than 5.5ms. Probably about 4.8ms.
Your exposure time is "1/6000", or something near 0.2ms.
So the time between the earliest exposure of any part of the sensor to the latest exposure of any part of the sensor =
something less than 6ms, probably a bit less than 5ms.Definitely nowhere near the 15ms implied by "1/66" s.
JohnV, do you have a reference that supports the above conclusion?
Or a ref. that tells us how exif's IntegrationTime 0x0423 is measured or calculated?
I thought the image I posted explained that "Integration Time" is equal to 'exposure time' plus 'readout duration' ...
-
@xpatUSA has written:
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
I don't know of any cameras with a focal plane mechanical shutter that can be read out as rapidly as your drawing indicates.
-
@JimKasson has written:@xpatUSA has written:
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
I don't know of any cameras with a focal plane mechanical shutter that can be read out as rapidly as your drawing indicates.
There aren't any times on that diagram.
It looks to be exactly like a diagram of the timing of an exposure using electronic shutter, on a camera which reads a row at a time - a typical Active-Pixel CMOS sensor.
In the case illustrated, the exposure time is longer than the (readout-speed limited) (electronic) shutter travel time, so there is a window when the entire sensor is exposed, and the vendor says this is where you should put your flash pulse if you want uniform flash illumination.
We could draw a nearly identical diagram for a film SLR with a mechanical "focal-plane" shutter, when the shutter speed is slower than the X-sync speed.
I have used industrial video cameras in exactly the manner illustrated. The flash freezes the (fast-moving) production line, and gives the effect of global shutter.
-
@JohnVickers has written:@JimKasson has written:@xpatUSA has written:
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
I don't know of any cameras with a focal plane mechanical shutter that can be read out as rapidly as your drawing indicates.
Yes you do! 😀
There aren't any times on that diagram.
It looks to be exactly like a diagram of the timing of an exposure using electronic shutter, on a camera which reads a row at a time - a typical Active-Pixel CMOS sensor.
In the case illustrated, the exposure time is longer than the (readout-speed limited) (electronic) shutter travel time, so there is a window when the entire sensor is exposed, and the vendor says this is where you should put your flash pulse if you want uniform flash illumination.
We could draw a nearly identical diagram for a film SLR with a mechanical "focal-plane" shutter, when the shutter speed is slower than the X-sync speed.
I have used industrial video cameras in exactly the manner illustrated. The flash freezes the (fast-moving) production line, and gives the effect of global shutter.
I don't know of any mechanical FP shutters that move slowly enough that sensor readout can take place in the time it takes for the shutter to scan the frame. So I don't need the timings on the drawing.
-
@JimKasson has written:@xpatUSA has written:
After using better search terms, I found it to the time between the first opening of the "slit" to the closure of the last slit in a rolling shutter.
Meaning that, when set to high speed over the 'sync' speed, the rolling shutter effect would still be possible from a moving object..
it has written:Although all rows are exposed for exactly the same period of time, the point in time for each row's exposure is slightly different. Each row [is] caught the scene at a slightly different point in time. As a result, moving objects in the scene may appear distorted. This is called the "rolling shutter effect".
Ref: www.1stvision.com/cameras/IDS/IDS-manuals/en/basics-shutter-mode.html
One would naïvely think that "Integration time" is also the camera 'sync speed', but not so on my camera which lists 1/180sec in the spec.
I don't know of any cameras with a focal plane mechanical shutter that can be read out as rapidly as your drawing indicates.
I doubt that their drawing is to scale.
Jim, do you have a reference that tells us how exif's IntegrationTime 0x0423 is measured or calculated?..
-
@xpatUSA has written:
Jim, do you have a reference that tells us how exif's IntegrationTime 0x0423 is measured or calculated?
Sorry, I don't
-
@xpatUSA has written:
I doubt that their drawing is to scale.
Are you saying the time axis is nonlinear? You are talking about the mechanical shutter in your camera, right?