I think he means to have a continuous function spatial domain and in the frequency domain. Then the pitch of the samples would determine the Nyquist frequency. But there are many ways to fit a continuous function to a set of sample points.
-
-
The Whittaker-Shannon interpolation formula en.wikipedia.org/wiki/Whittaker%E2%80%93Shannon_interpolation_formula converts samples into such a function; then you take the absolute value of the FT, if there is no aliasing. There are more practical but less precise interpolation formulas, of course.
If there is aliasing, it "folds" higher frequencies back, then you have to subtract that range below Nyquist where you might get folding. You may not get it in some parts of the image, but you would never know what is real and what is not.
-
@JimKasson has written:@xpatUSA has written:
I'm confused ... how can a continuous function have a "Nyquist"?
I think he means to have a continuous function spatial domain and in the frequency domain. Then the pitch of the samples would determine the Nyquist frequency. But there are many ways to fit a continuous function to a set of sample points.
Right, that is why used quotation marks. What is "continuous" is the domain - it is a function of a non-discrete variable, vs. a function on a grid.
-
@JACS has written:
The Whittaker-Shannon interpolation formula en.wikipedia.org/wiki/Whittaker%E2%80%93Shannon_interpolation_formula converts samples into such a function; then you take the absolute value of the FT, if there is no aliasing. There are more practical but less precise interpolation formulas, of course.
If there is aliasing, it "folds" higher frequencies back, then you have to subtract that range below Nyquist where you might get folding. You may not get it in some parts of the image, but you would never know what is real and what is not.
We can eliminate aliasing in both cases by picking the right target. Would you then expect significant differences?
-
@xpatUSA has written:
At Nyquist, the 3MP won hands-down, as should be expected of course.
Especially if it is 3.4MP and has no microlenses, but is that "resolution", or is it an artifact of trying to apply a naïve analog metric to an aliasing sampler with blind alleys between rows and columns of pixels, which increases contrast?
-
@LeeJay has written:
A while back, someone demanded a 300dpi image when I sent them a 72dpi image (at 12MP). So I sent them a 4 pixel image at 300dpi.
It will save them money on ink!
-
@xpatUSA has written:Jim has written:
So if we’re looking at MTF in cycles per millimeter as our definition of resolution, 16-shot pixel shift buys us no resolution at all
And with my two different cameras and - yes - lenses, it should have come as no surprise at all.
The advantage at Nyquist went also to the 3MP with it's 54% fill factor and no microlenses and no AA filter. Best possible MTF at Nyquist being a theoretical 80% or so - as opposed the more common 64% or less.
Downsize it to 50% with nearest neighbor, and it may do even better.
-
@LeeJay has written:
A while back, someone demanded a 300dpi image when I sent them a 72dpi image (at 12MP). So I sent them a 4 pixel image at 300dpi.
Sure you don't mean PPI in all three cases? DPI applies to halftoned images.
-
@xpatUSA has written:
Yet, when I change the PPI in an image, it still looks the same on my screen ...
If the image is also not resampled when you change the PPI then yes. If it is resampled then it might or might not look the same depending on how much smaller in pixel count it is after the PPI is changed.
In a Web browser an image's width on the web page will be whatever width has been set for the image in the web page's CSS.
-
@DannoLeftForums has written:
If the image is also not resampled when you change the PPI then yes. If it is resampled then it might or might not look the same depending on how much smaller in pixel count it is after the PPI is changed.
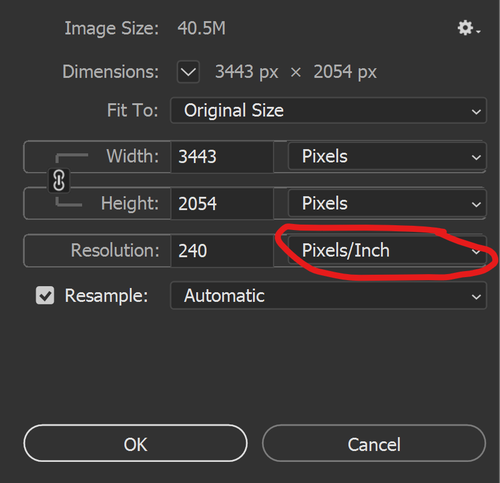
Illustration (see red outline of relevant control in Ps):
-
@JimKasson has written:@DannoLeftForums has written:
If the image is also not resampled when you change the PPI then yes. If it is resampled then it might or might not look the same depending on how much smaller in pixel count it is after the PPI is changed.
Illustration (see red outline of relevant control in Ps):
Yes, the same checkbox option is also in Photoshop Elements and I would expect it to be in any image resizing app.
-
@DannoLeftForums has written:@xpatUSA has written:
Yet, when I change the PPI in an image, it still looks the same on my screen ...
If the image is also not resampled when you change the PPI then yes. If it is resampled then it might or might not look the same depending on how much smaller in pixel count it is after the PPI is changed.
Well, I would argue (and people may disagree) that the PPI is meta-data only, and you can always change it freely with no effect on the image itself until it comes time to print. Then it matters, of course, because the printer will try to respond to it.
If the image is resampled, I suggest you are doing two separate operations -- changing the PPI value in the meta-data, and then changing the image size using the combination of X, Y, and new PPI values to define the new image size. But these are really two things, although that's obscured slightly by the fact that many popular applications put them all in the same dialog box.
-
@chd has written:@DannoLeftForums has written:@xpatUSA has written:
Yet, when I change the PPI in an image, it still looks the same on my screen ...
If the image is also not resampled when you change the PPI then yes. If it is resampled then it might or might not look the same depending on how much smaller in pixel count it is after the PPI is changed.
Well, I would argue (and people may disagree) that the PPI is meta-data only, and you can always change it freely with no effect on the image itself until it comes time to print. Then it matters, of course, because the printer will try to respond to it.
If the image is resampled, I suggest you are doing two separate operations -- changing the PPI value in the meta-data, and then changing the image size using the combination of X, Y, and new PPI values to define the new image size. But these are really two things, although that's obscured slightly by the fact that many popular applications put them all in the same dialog box.
Yes, I generally agree.
PPI is mainly used to size images to a physical print size. It has no effect on online displays unless the image is also resampled and then as described earlier.
-
@JimKasson has written:@JACS has written:
The Whittaker-Shannon interpolation formula en.wikipedia.org/wiki/Whittaker%E2%80%93Shannon_interpolation_formula converts samples into such a function; then you take the absolute value of the FT, if there is no aliasing. There are more practical but less precise interpolation formulas, of course.
If there is aliasing, it "folds" higher frequencies back, then you have to subtract that range below Nyquist where you might get folding. You may not get it in some parts of the image, but you would never know what is real and what is not.
We can eliminate aliasing in both cases by picking the right target. Would you then expect significant differences?
Now you are talking about how we measure it but first we need to understand what it is that we want to measure. If you think of resolution as being the extinct one (you do not care about contrast at it as long as it is not too small), then you do not need to do the interpolation, as I indicated above; the answer is the Nyquist limit of the sensor assuming the softening along the way (diffraction, etc.) reaches it. If you project a higher resolution physical image, that is bad but the sensor can resolve up to that limit. In that sense, the myth is not a myth.
If you are interested in the resolution of the whole chain: lens + sensor stack + sensor, then we can define the extinct resolution as the highest one possible without aliasing, i.e., either Nyquist or less if the lens restricts it. Then the slanted edge is as good as choosing, say a sinusoidal target below Nyquist only up to Nyquist, and that gives you the maximal resolution you can get if you avoid aliasing (say your scene has no frequencies too high, or there is some shake, etc.). It gives you the contrast as well. Everything above Nyquist is not resolution, and can hurt it if your scene has frequencies that can be aliased. If your scene is "soft," it is good to see something significant above Nyquist in the measurements but that does not help by itself; it indicates a strong contrast just below it.
-
@JimKasson has written:@LeeJay has written:
A while back, someone demanded a 300dpi image when I sent them a 72dpi image (at 12MP). So I sent them a 4 pixel image at 300dpi.
Sure you don't mean PPI in all three cases? DPI applies to halftoned images.
That's what it actually is, but since Photoshop, Lightroom and EXIF data all call it "dpi", so do I.
-
@LeeJay has written:@JimKasson has written:@LeeJay has written:
A while back, someone demanded a 300dpi image when I sent them a 72dpi image (at 12MP). So I sent them a 4 pixel image at 300dpi.
Sure you don't mean PPI in all three cases? DPI applies to halftoned images.
That's what it actually is, but since Photoshop, Lightroom and EXIF data all call it "dpi", so do I.
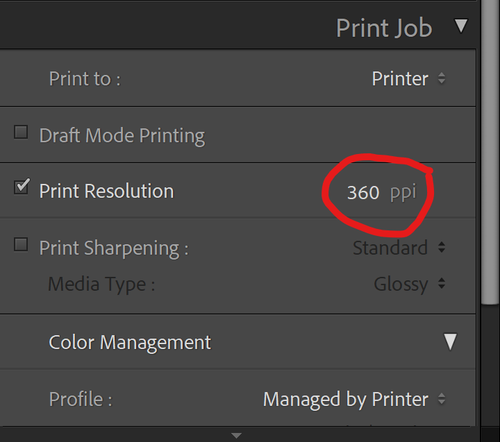
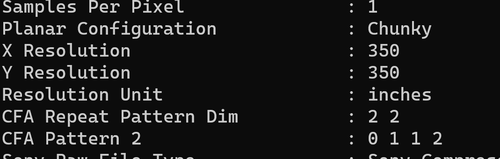
Lightroom:
Photoshop:
EXIF:
-
I've never really understood this 'pixel/inch stuff. A photo has a certain number of X/Y pixels. There's no distance involved with that.
If you display it on a screen the actual pixels displayed will be however many the screen can support and the display s/w will manage that.
If you print it, the printer can do x pixels/inch - depends on the print head and what it is capable of. So, depending on the size of the photo paper, there will be interpolation up or down to fit the paper. By "forcing" something to do a pixels/inch output, you are just introducing an extra uncessary step which may make the image look worse (and I doubt it would ever make it look better).
Just my thought.
Alan
-
Not wishing to hijack the thread, but a quick aside...
Why "per inch"? Is this just a UK/USA thing or does the whole world use imperial measures for printing?
Tim