[deleted]
-
-
I was going to post this in search of clarity ...
... but when I scrolled down, Tom had already commented there no less than six times recently!
-
@xpatUSA has written:@DavidMillier has written:
[quote="@TomAxford"]
Quoted message:It should be clear that “wide-angle perspective” and “telephoto perspective” are imprecise terms, since perspective relates only indirectly to the actual lens focal length. True perspective depends only upon the camera-to-subject distance.<big snip>
It seems to me that you are suggesting you can achieve these affects simply by changing your viewing position relative to the print. It would be interesting if you could generate all these perspective effects (Big Nose Effect, Layered Collage Effect) just by changing the viewing distance from the print.
Is that what you are saying you can do, or am I simply misunderstanding the 10k words you must have written on the subject by now (more than possible!)?
Cheers
Dave
I was going to post this in search of clarity ...
... but when I scrolled down, Tom had already commented there no less than six times recently!
I think a simplified rule of thumb is all you need to control perspective as a photographer:
"Select a focal length that magnifies the background to whatever size you need. Then move your feet towards or away from the foreground to get that the size you need"
-
@JACS has written:
It cannot be possibly a fallacy before you define what perspective means.
Here is how science, or at least math works. You define your notions, state your assumptions, state your claims, and then you prove them. How do I know that? - I have done it > 100 times, quite successfully. Ansel Admas did not write a science book, you cannot expect such a logical structure to be followed rigorously. Still, he gives some notion of what he thinks perspective is. *It is not what you think he thinks it is. * Here is a link to his book:
subhadip.ca/alluploads/books/bengali/the-camera-ansel-adams-series-no-1.pdf
On p.98, he talks about converging lines, objects that appear larger, etc. He considers a photo a 2D thing, which it is. He is not concerned with a viewer.
You call yourself a scientist yet you are unable to produce a rational scientific argument to support the claims that Ansel Adams made. If you go back to the full quote I gave in the OP, it is very clear that he was claiming that telephoto perspective and wide-angle perspective were due to the camera position and not the viewer's position (which he never mentions).
You are blustering and trying to divert attention rather than giving a rational scientific argument.
The truth is that telephoto compression and wide-angle perspective distortion depend primarily on how the image is viewed relative to its centre of perspective (which depends on the focal length and degree of enlargement).
-
[deleted]
-
@JACS has written:@TomAxford has written:
You call yourself a scientist yet you are unable to produce a rational scientific argument to support the claims that Ansel Adams made. If you go back to the full quote I gave in the OP, it is very clear that he was claiming that telephoto compression and wide-angle distortion were due to the camera position and not the viewer's position (which he never mentions).
Actually, it is not "very clear." First, "wide-angle distortion" does not appear there at all. You are putting words in his mouth. What he calls "flatness" is an empirical fact. Such images appear flat regardless of the position of the viewer. This is not geometry, it is human perception. You said that yourself by asking us to imagine that we are looking through a small window and forget that we are looking at a photo. Well, it is a photo, and he is right, this is what most of us see. I can display such an image on my phone and put it 2m away from me - it still looks flat.
Quoted message:You are blustering and trying to divert attention rather than giving a rational scientific argument.
The truth is that telephoto compression and wide-angle perspective distortion depend primarily on how the image is viewed relative to its centre of perspective (which depends on the focal length and degree of enlargement).
First, it is not "the truth," see above. Next, he does not even claim what you think he does.
You are going round in circles. Read my thread on perspective distortion.
I have edited my previous post to use the terms wide-angle perspective and telephoto perspective instead of wide-angle distortion and telephoto compression which are often used to refer to the same effects. It does not change my argument.
I am not going to discuss this with you further. If you think you can present a credible scientific explanation for what people colloquially refer to as telephoto compression, then please do so in a thread of your own. I look forward to reading it.
-
@JACS has written:
What he calls "flatness" is an empirical fact. Such images appear flat regardless of the position of the viewer. This is not geometry, it is human perception. You said that yourself by asking us to imagine that we are looking through a small window and forget that we are looking at a photo. Well, it is a photo, and he is right, this is what most of us see. I can display such an image on my phone and put it 2m away from me - it still looks flat.
Don't be so sure. Did you try? But at 10 meters? (Assuming you can see any details then...)
But human perception is involved too, this I don't oppose. We have used to typical image sizes and scenes and often correct some [perspective] distortions unconciously. We may not process scene, visible through window, in the same way - thereby I actually can't say, will your tiny flat image on faraway phone screen and exactly same scene, seen through small window at correct distance, preceived similarly. Or the same scene, viewed without window in its entirety...
Geometrically all they should be identical, perceptually they probably are not. -
[deleted]
-
[deleted]
-
@TomAxford has written:
However, longitudinal magnification is not relevant to the perspective in the two-dimensional image captured by the sensor.
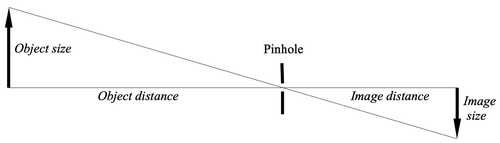
That can be seen very easily by considering a pinhole camera. It has no lens and has no longitudinal magnification, yet it produces an image with the same linear perspective as a camera with an ordinary rectilinear lens. Longitudinal magnification is irrelevant to perspective in 2-D images.
The mathematics of linear perspective is summed up in the equation:
So in the above, if any size of print is made from the film, then the optimum viewing distance is that which subtends the same object angle as from the pinhole to the film, if I understand correctly. And by similar triangles, the ratio (object size / object distance) is all one needs to figure the viewing distance for any size of print (or any zoom on one's monitor).
Say a 30 ft tree at 100 yds subtends about 0.1 rad. Ergo, if the tree shows up as 2 in. on a monitor, then the optimum viewing distance is about 20 in ... but, if I zoom out to see more of the scene, I should move closer! Who actually does that, I wonder?
-
@JACS has written:
I downsized my browser view to 25%, down from 125%. It is a 4K laptop, so the image becomes the size of my thumb. Then I leaned way back. Those trees look like growing off the head of the girl - it looks fake perspective wise, even viewed this way.
I played a bit more - I dowsized image (Lisa 200 in fact - trees are clearer there) and attempted to place it into one of NCV architecture shots, like a small window.
I'll attach resulting image, but not as preview - I have not asked NCV about reposting rights :(There appears very interesting effect.
Initially this attempt-to-be-a-window looked like TV set and this way it was perceived flat.
Then I attempted to imagine that this is window - and now objects shifted in perspective (only in my mind!); image feels more like Lisa 105 :)
(I have no good background image with real small window - if you find one, we can experiment further. It likely needs to be perceived as real window, not some TV set.)Both Lisas are also included in attached image, they somehow helped seeing result as look through window.
-
Here are two more example images to exercise the little grey cells of those who are interested in perspective and how we see it.
The first is a multiple-exposure image from Wikimedia. It illustrates a number of common cues that our brains use to see depth in a 2-D image.
The size of the last girl is about one fifth the size of the first girl, which information our brain uses to perceive the last girl as about five times as far away as the first.
In the next image I have created a small inset which is a copy of the original image at around 1/7th the size. The perspective matches sufficiently well to create a credible image of ten girls running along the path. The 6th girl is about 1/7th the size of the first and the last girl is less than 1/30th the size of the first. The distance between the 6th and 10th girls appears to be about 7 times as much as the distance between the 1st and 5th girls. Yet the inset image is an exact copy of the original image, just reduced in size.
Here is another little puzzle about the perspective: why does the 6th girl look as if she is veering off to her left, rather than running straight along the path?
-
I'll bite, if I can get my words right...
Because the track is not parallel to the line of sight of the camera, each point on the track has a different angle to the camera. The closer the girl, the greater the angle between her and the line of sight. The 6th girl, being a copy, is still pointing in a direction with the same angle as the first, while if she was real, her angle would actually be on the other side of the 90 degree point of intersection.
Question: If there were really 10 girls roughly equally spaced, and not a resized copy, would the distance between the 6th and 10th still appear to be much greater than the 1st and 5th?
I think I have answered it for myself.
-
@Bryan has written:
Question: If there were really 10 girls roughly equally spaced, and not a resized copy, would the distance between the 6th and 10th still appear to be much greater than the 1st and 5th?
No.
-
[deleted]
-
@JACS has written:@TomAxford has written:
In the next image I have created a small inset which is a copy of the original image at around 1/7th the size. The perspective matches sufficiently well to create a credible image of ten girls running along the path. The 6th girl is about 1/7th the size of the first and the last girl is less than 1/30th the size of the first. The distance between the 6th and 10th girls appears to be about 7 times as much as the distance between the 1st and 5th girls. Yet the inset image is an exact copy of the original image, just reduced in size.
Here is another little puzzle about the perspective: why does the 6th girl look as if she is veering off to her left, rather than running straight along the path?
The resolution is so low, plus the mistake pointed out above, hard to say if it really looks that way. The main reason, if it does, would be that, well, the perspective is different. If the girl was really that far, we would have a mostly frontal view.
It is a pity that the example is not something like a railroad line or simulation thereof. Then the effects of zooming, resizing and pasting, cropping or windowing, etc. would be more easily understood ...
-
[deleted]
-
@JACS has written:
Here we go. I had to fight the auto-snap feature in PS, so the alignment is not as good as I want it to be.
Thanks!! Took me a minute to two notice the inset which preserves the viewpoint lines of perspective but breaks another rule or two e.g. foreshortening.