What is telephoto compression (perspective compression)? Tom Axford 2023

This post takes a different approach to explaining telephoto compression that does not rely on our perception of depth in an image, but is grounded solely in mathematics and optics. The results can also be confirmed by experiment, no personal judgement is required!

Linear Perspective
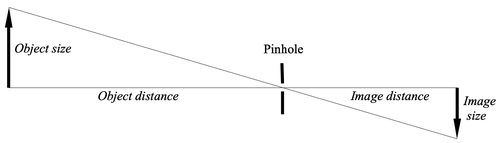
A pinhole camera creates images as shown in the diagram below:

The pinhole is at the centre of perspective, also called the centre of projection. This type of perspective is called linear perspective when used in works of art such as paintings and drawings. Simple geometry gives us the basic equation that characterises linear perspective:

object size / object distance = image size / image distance

A camera with a rectilinear lens creates exactly the same perspective, the image distance now being the focal length of the lens, so we can rewrite the equation as:

object size / object distance = image size / focal length

Telephoto Compression
By the above equation, if the object size and distance remain the same, increasing the focal length will cause the image size to increase in proportion.

On the other hand, if the object distance is varied while keeping the focal length and object size unchanged, then the image size will vary in inverse proportion to the object distance.

Hence, multiplying the focal length by a factor, n, has exactly the same effect on the image as dividing the object distance by the same factor, n. If the scene contains objects at different distances, each object distance must be divided by n.

In other words, increasing the focal length produces an image that is exactly the same as one in which all object distances have been compressed by the same factor as the focal length was increased by. This effect is commonly called perspective compression or telephoto compression.

An Example
Consider the effect of changing the focal length from 50mm to 100mm. This will double the size of the image of every object in the field of view. So the photo taken at 100mm is exactly the same as the photo taken at 50mm magnified by 2, but with a smaller field of view.

However, the photo taken at 100mm focal length is also exactly the same as a photo taken at 50mm focal length but with all object distances halved. Suppose the 100mm photo is of two objects at distances of 100m and 50m from the lens. If we take a photo using 50mm focal length with these two objects placed at 50m and 25m from the lens, we should get exactly the same image (assuming the two objects appear on a featureless background).

To make it easier to do this experiment, I have used two matchboxes at 100cm and 50cm distance for the photo with 100mm lens (on the right) and the same two matchboxes at 50cm and 25cm for the photo with the 50mm lens (on the left). My measurement of distances was very approximate, but the two shots are nearly identical (ignoring the background, which I could not easily move).

[deleted]

Hi Tom.

Thank’s for this detailed thread about the so called „compression effect“.

I have a comprehension question about your statements.

But before I ask this question, please watch the photo below and give me your first glance depth perception/distance estimation. All the other readers are also welcomed to give their estimations.

Shown are two fluffy koalas with an identical physical size (height of each is approx. 30 cm).

Imagine you are in that scene, sitting in front of the table at the same position where the camera stood and looking at the koalas:

How far away from you do you perceive the first koala and the second koala?

How large do you perceive the distance between them?

As said: Of interest is only your subjective first-glance-impression about the subjective perceived distances and not a technical calculation of the real camera-to-subject-distance.

So again: What is your subjective impression?

Thank’s in advance for your valued time and input.

Regards
Mike

I'd guess that I'm 2 m away from the first Koala and 4 m from the second Koala, making the distance between them 2 m!

Giving a first glance impression of distance is very difficult. The image comes up initially quite small (17cm diagonal) and I am viewing from 50 to 60cm away. It's is extremely difficult to judge both size and distance. If I blanked out the surroundings completely, then I would probably think that the koalas are much smaller than 30cm high. However, looking at the surroundings and knowing the typical size of room fittings and furniture makes them look more like 30cm high.

The best way to estimate distance is then to compare the angular size of the koalas to the angular size of other objects in my field of view. That makes them look a long way away, much further away than I would think is the case, judging by the parts of the room that are visible in the picture. Of course, this is explained by the fact that my viewpoint is much further away than the centre of perspective.

The right way to do it is to view the image from the centre of perspective. To do this, I enlarged the image to a diagonal size of 63cm and viewed it from that distance away. Then, by comparing the angular size of the koalas with that of similar size objects elsewhere in my field of view, I would estimate the distances to be about 2m and a bit less than 4m away. Estimating distances in real life is always difficult unless you can compare with similar size objects at known distances away. Most people are surprisingly bad at estimating distances unless they have trained themselves to do so.

With photos, it is sometimes helpful to shut one eye (which stops your binocular vision telling you how far away the photograph is). Even so, it is still very hard to imagine that you are looking at a real scene rather than simply a 2-D picture. The best way is probably to make a print and hold it in front of you so you can directly compare it with the real scene, the way painters do when they are painting the scene in front of them.

[deleted]

Thank’s a lot for your replies; I really appreciate it.

Below is a second picture, and I am asking again for your pure subjective distance perception and estimation at a first glance.

Important: Forget all the technical stuff like focal length, field of view, angle of view etc. and try to forget also the first picture. That is not a competition to find the person with the best estimation skills. It’s all about to find out the first distance-thoughts your brain emits when viewing the picture.

So, imagine you are personally in the scene: How far away do you perceive the koalas from you, how large do you perceive the distance between them?

Based on viewing the image at full size from about the length of the diagonal, my impression is that the two koalas are something like 1m and 2m from the camera. However, that is largely based on the information gained from your previous post that the koalas are about 30cm high. If that information was not known, then it is very difficult to judge both the size of the koalas and their distance away.

I'm more likely to guess the size of the table and use that to estimate the koala's size and hence distance away.

Gut feeling: I'm 1 m away from the Koala in the front and 3 m from the Koala in the back. So the distance between them is still 2 m.

Thank's for the replies.

Does your distance perception change if you shrink the last picture? (with shrinking I don’t mean cropping or changing aspect ratio; I mean downsizing the entire picture/watching a smaller version of it with the same viewing distance).

Does your distance perception of the full screen picture change if you increase your personnel viewing distance to your screen? Or does your distance perception change if you look at your screen not centrally but sidewards?

To be more precise what I mean:

You watch the last picture of the koalas in full screen mode on your desktop monitor and exempli gratia you perceive the distance to the first koala as 1 meter and to the second as 2 meter (or maybe 3 meter) and the gap between them as 1 meter (or maybe 2 meter).

Now you minimize the entire picture, maybe by factor 0.5 or you double your viewing distance to the screen.

Does your distance perception change in that case that you say to yourself exempli gratia: When I shrink the overall picture or when I double the viewing distance, I get the impression, that the first koala is now 2 meters away from me, the second one 4 meters (or maybe 6 meters)? And do you get the impression that the gap between the koales increases/decreases with a change in viewing distance/picture size?

BTW: You can do the same with the first picture and ask yourself if pictorial distance perception changes with a change in relative viewing distance.

NB: you find the original photos in the attachments at the bottom of my posts.

Much obliged.
Mike

No, in my case it doesn't. Still feel like I'm around 1 m away from the first and 3 m from the second.

(Same with the first image, however it's getting a bit harder to judge there the smaller it gets...)

Yes, it does change, but not if you are "seeing" it as purely an image that is being shrunk. You have to try to imagine that you are looking at a real scene, not just at a two-dimensional photograph.

It is often easier to imagine that you are looking at a real scene when viewing a moving image. Have a look at the second video in this article. Zooming the lens is the same as shrinking or expanding the image. When the lens is zoomed back to a shorter focal length the image is shrunk. This makes the distances from the camera appear greater, so the train appears to be moving faster.

Most people see the illusion of the train moving faster even if they do not consciously "see" the distances increasing when a still image is shrunk.

Another situation in which the perspective seen by the viewer is particularly important is the rear-vision mirrors (or cameras) in a car. My car has four: one mirror at the top-centre of the windscreen (which gives a normal perspective), two side mirrors (which give wide-angle views) and a rear-view camera for reversing (which gives an ultra-wide-angle view). The wide-angle views make things appear further away than they really are and the driver needs to make allowance for this when reversing.

[deleted]

When I am looking at a photograph of a real scene, I always imagine that I am looking at the real scene. My brain does all the hard work to interpret the „pictorial depth“; it is some kind of unconscious inference that happens. The pictorial depth cues are so strong for me, that it is nearly impossible to ignore them and to identifiy the picture as that what it really is: bits, bytes and pixels without any depth.

Imaginging that I look at a real scene and not simple „seeing“ it as purely a flat image, my depth perception does not change with a change in relative viewing distance (h.e. shrinking the entire picture and/or increasing the viewing distance to my display).

And I think simplejoy and JACS share my impression.

But maybe your perception has problems with the shrinking process itself. So please try the following: Look at the picture in full screen mode and with your usually viewing distance to the screen, then place yourself farther away, look again at the full screen image and – of course – imagine you are in the scene: Does your depth perception have changed? Do you perceive the koalas now farther away?

You are clearly having difficulty in "seeing through" the 2-D picture to imagine the real scene that the image represents.

I suggest that you try a completely different situation. While driving your car down a busy highway, glance in the side mirror to look at the traffic behind. The side mirror is usually curved to give a wide-angle view. This shrinks the size of the image that you see and makes distances look much greater than they really are (it's not difficult to prove that mathematically). It should be obvious that distances look greater in the wide-angle mirror, although we soon learn to make allowances for these greater distances and not do something likely to cause an accident.

The central rear view mirror usually reflects a normal image with no change of perspective; so we can judge distances nearly as easily in that mirror as we can when looking ahead at the vehicle in front. The difference in perspective between the image seen in the central mirror and the side mirrors should be obvious.

I would not want to be a passenger in a car driven by someone who was unaware of the difference!

Tom, you made an interesting point with the rear-view-mirrors.

This thread is very overloaded with more than 120 posts.

Should I start a new thread to get more feedback? What do you think?

Yes, that seems like a good idea. I think it gets more difficult to look at threads when they get very long.

Hi Tom.

I am preparing a new thread related to the compression effect, but it is very time consuming due to the complexity of the theme and due to the fact that I am not a native English speaker (it’s hard to get all the correct termini technici).

Please could you tell me how I can embed pictures in my text that way, that one can click on it and it then pops of in a new window, like yours of the brick house. I mean, if you click on my koala pics you get not the pic in a new window, instead one get directed to the upload site, that’s annoying.

BTW Yesterday I worked through all the more of 120 posts and replies following your thread which is a brutal tour de force due to the huge amount of information mass.

I came across this post, that unfortunately did not get much regard:

I think this guy is on the right track.

Regards
Mike

I click on the upload file icon (the up-arrow symbol which is second-last in the list of editing icons at the top of the message window. Then click on insert icon next to the name of the image file at the bottom to put a smaller version of the image into the text.